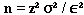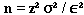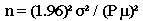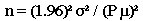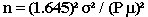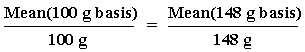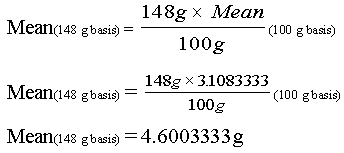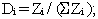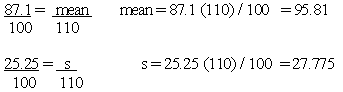MANUAL
Guidance for Industry: Guide for Developing and Using Data Bases for Nutrition Labeling March 1998
- Docket Number:
- FDA-2020-D-1961
- Issued by:
-
Guidance Issuing OfficeCenter for Food Safety and Applied Nutrition
More Food Labeling and Nutrition Guidance Documents
For updated examples of nutrition labels see Examples of Revised Nutrition Facts Panel Listing Trans Fat.
Table of Contents
Foreword: Purpose of the Manual
Chapter I: Introduction and Background
- What Are Nutrition Labeling Data Bases?
- Manufacturer's Responsibility
- Submitting Data Bases to FDA is Voluntary
- How Compliance Works -- Title 21 of the Code of Federal Regulations (21 CFR 101.9(g))
- Why Submit a Data Base to FDA?
Chapter II: How to Develop a Nutrition Labeling Data Base
- Characterizing the Product(s)
- Designing a Sampling Plan
- Collecting the Sample Units
- Analyzing the Laboratory Test Samples
- Statistically Analyzing the Data and Interpreting the Results
Chapter III: Ingredient Data Bases
Chapter IV: The FDA Data Base Review Process
Formulas may not show up correctly in text browsers. Please use a graphical browser or request a printed copy of this document from the address at the bottom of the page.
Foreword: Purpose of the Manual(1)
This manual is a guidance document. It has been written by the Center for Food Safety and Applied Nutrition (CFSAN) at the Food and Drug Administration (FDA) to assist industry in the task of preparing nutrient information for labels (see sample below) and labeling that meets the requirements of FDA regulations. This manual gives generic instructions for developing and preparing an acceptable data base, as well as the recommended statistical methodology to develop nutrition label values. A manufacturer, trade association, or other data base developer may follow the guidelines presented here or may choose to use alternative procedures not provided in this document. FDA recommends that those choosing to use alternative procedures discuss the procedures further with the agency to prevent expenditure of resources and effort on activities that may later be determined to be unacceptable to FDA.
FDA is committed to working with all interested parties to achieve reliable nutrition labeling data in the most economical fashion. The agency acknowledges that following all of the recommendations/guidance in this manual could pose an economic hardship. Therefore, in certain instances, FDA may accept a proposal to develop a data base over several years to help defer costs. This manual also includes FDA's policy statement regarding its data base review process. The agency has modified its review process in response to concerns expressed by industry.
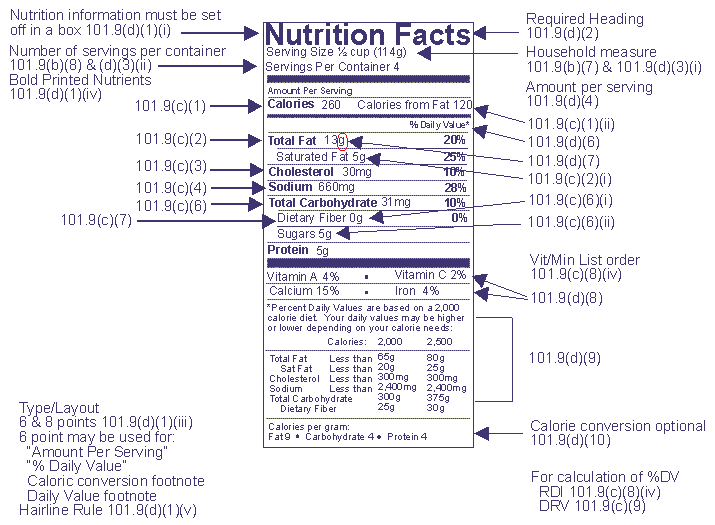
The Nutrition Label
Nutritional information is based on product as packaged 101.9(b)(9)
Chapter I: Introduction and Background
Over 25 years ago, the Food and Drug Administration (FDA) initiated regulatory activities directed toward the development of regulations for nutrition labeling of food products. In 1973, FDA published the first regulations that required the nutrition labeling of certain foods: those with added nutrients and those for which a nutrition claim was made on the label, or in labeling or advertising. However, it wasn't until the 1990's that regulations promulgated under the authority of the Nutrition Labeling and Education Act of 1990 (NLEA) expanded mandatory nutrition labeling to virtually all foods regulated by FDA. In response to these regulations, industry has expressed greater interest in creating nutrition labeling data bases.
What Are Nutrition Labeling Data Bases?
Nutrition labeling data bases are generally collections of nutrient data for specific products or commodities, which are compiled by a manufacturer, organization, or trade association representing a group of manufacturers. The majority of the nutrition labeling data bases that industry has submitted to FDA for review fall into the "finished food" category. The submitted data are supported and accompanied by documentation that describes the sampling strategies, analytical methodology, and statistical treatment of data.
Another type of nutrition labeling data base is an ingredient or "recipe" data base that is comprised of nutrient data from several sources. For such data bases, software is used to calculate label values derived from the nutrient content of ingredients that comprise a product's recipe, while taking into account nutrient losses during processing.
Nutrition labeling data bases are proprietary. They are owned by the developer and are seldom publicly available. Proprietary nutrition labeling data bases developed by industry and submitted to FDA for review should not be confused with data available from the scientific literature or commercially available software.
Manufacturer's Responsibility
FDA's continuing policy since the 1970s assigns the manufacturer the responsibility for assuring the validity of a product label's stated nutrient values. Accordingly, the source of the data used to calculate nutrition label values is the prerogative of the manufacturer, but FDA's policy recommends that the nutrient values for labeling be based on product composition, as determined by laboratory analysis of each nutrient. FDA continues to recommend the use of the Official Methods of the Association of Official Analytical Chemists International (AOAC), with non-AOAC Official Methods used only in the absence of appropriate AOAC validated methods. For each product that is included in a nutrition labeling data base submitted to FDA, the agency requests that the developer include a table identifying proposed analytical methods that were used in the analysis of each nutrient, with accompanying information containing validation of the method used by the onsite or commercial laboratory for the matrix of interest.
Submitting Data Bases to FDA is Voluntary
Although FDA encourages industry to submit nutrition labeling data bases to the agency for review, submission of a data base to FDA for the purpose of nutrition labeling is voluntary. The agency has not and does not intend to prescribe how an individual company is to determine nutrient content for labeling purposes.
How Compliance Works -- Title 21 of the Code of Federal Regulations (21 CFR 101.9(g))
FDA analyzes food samples that have been randomly collected from lots to determine compliance with labeling regulations. The agency defines a food lot as a collection of the same size, type and style of the food that is designated by a common container code or marking, or that constitutes a day's production. The sample for nutrient analysis shall consist of a composite of 12 subsamples (consumer units), taken 1 from each of 12 randomly chosen shipping cases. FDA will then analyze the nutrient content of this 1 composite test sample.
The agency generally analyzes composites by appropriate methods found in the most recent edition of Official Methods of Analysis of AOAC International (AOAC International, Gaithersburg, MD, 16th edition, 1995, and yearly revisions/updates) (see below for additional information on selection of methods). The ratio between the nutrient level derived by analytical testing and the label value is calculated to determine whether the nutrient in question is in compliance with applicable regulations. The ratio is defined as:
(laboratory value / label value) x 100 = %
In order to evaluate the accuracy of nutrition label information against a standard for compliance purposes, FDA regulations define two nutrient classes (Class I and Class II) (21 CFR 101.9(g)(3)) and list a third group (Third Group) of nutrients (21 CFR 101.9(g)(5)). Class I nutrients are those added in fortified or fabricated foods. These nutrients are vitamins, minerals, protein, dietary fiber, or potassium. Class I nutrients must be present at 100% or more of the value declared on the label ; in other words, the nutrient content identified by the laboratory analysis must be at least equal to the label value. For example, if vitamin C is added in a fortified product and the label states that vitamin C is present at 10% Daily Value (DV), the laboratory value must equal at least 6 mg of vitamin C/serving (i.e., 10% of the 60 mg Reference Daily Intake (RDI) for vitamin C that is specified in 21 CFR 101.9(c)(8)(iv)). The ratio between a laboratory finding of 4.8 mg vitamin C/serving (i.e., 8% DV) and the label value of 10% DV would be calculated as follows:
(8% / 10%) x 100 = 80% or (4.8 mg / 6 mg) x 100 = 80%
and the label value would not be in compliance.
Class II nutrients are vitamins, minerals, protein, total carbohydrate, dietary fiber, other carbohydrate, polyunsaturated and monounsaturated fat, or potassium that occur naturally in a food product. Class II nutrients must be present at 80% or more of the value declared on the label. As an example: If vitamin C is a naturally occurring nutrient in a product, and the product declares 10% DV vitamin C (i.e., 6 mg/serving) on its label, then laboratory analysis must find at least 80% of the label value (80% of 6 mg or 4.8 mg vitamin C/serving) for the product to be in compliance.
The Third Group nutrients include calories, sugars, total fat, saturated fat, cholesterol, and sodium. However, for products (e.g., fruit drinks, juices, and confectioneries) with a sugars content of 90 percent or more of total carbohydrate, to prevent labeling anomalies due in part to rounding, FDA treats total carbohydrate as a Third Group nutrient instead of a Class II nutrient. For foods with label declarations of Third Group nutrients, the ratio between the amount obtained by laboratory analysis and the amount declared on the product label in the Nutrition Facts panel must be 120% or less, i.e., the label is considered to be out of compliance if the nutrient content of a composite of the product is greater than 20% above the value declared on the label. For example, if a laboratory analysis found 8 g of total fat/serving in a product that stated that it contained 6 g of total fat/serving, the ratio between the laboratory value and the label value would be (8 / 6) x 100 = 133%, and the product label would be considered to be out of compliance.
Reasonable excesses of class I and II nutrients above labeled amounts and reasonable deficiencies of the Third Group nutrients are usually considered acceptable by the agency within good manufacturing practices.
Why Submit a Data Base to FDA?
In accordance with 21 CFR 101.9(g)(8), compliance with the provisions set forth in 21 CFR 101.9(g)(1) through (g)(6) may be provided by use of an FDA approved data base that has been developed following FDA guideline procedures and where food samples have been handled in accordance with current good manufacturing practice to prevent nutrient loss. An approval is granted when FDA has agreed to all aspects of the data base in writing or when a clear need is presented (e.g., raw produce and seafood). Approvals are granted for a limited time and will be eligible for renewal in the absence of significant changes in agricultural or industry practices. Guidance in the use of data bases may be found in this document, the FDA Nutrition Labeling Manual--a Guide for Developing and Using Data Bases.
FDA published its policy concerning the review of data bases for use in the voluntary and mandatory nutrition labeling of foods in a final rule entitled "Guidelines for the Voluntary Nutrition Labeling of Raw Fruits, Vegetables, and Fish" in the Federal Register of August 16, 1996 (61 FR 42742). This policy is the most recent such statement of the policy made by the agency and will be referred to throughout the manual.
FDA states that upon submission of a data base, "firms are free . . . to begin use of the nutrient label values and to initiate the planned studies to collect and update nutrient values. During this interim period, FDA does not anticipate that it will take action against a product bearing label values included in a data base submitted to the agency for review. If any product is identified through FDA compliance activities as including label values that are out of compliance, contingent on the company's willingness to come into compliance, the agency intends to work with both the manufacturer and the data base developer to understand and correct the problem label values" (61 FR 42742).
Chapter II: How to Develop a Nutrition Labeling Data Base
FDA recommends five general steps that industry may choose to follow in the development of a nutrition labeling data base:
-
characterizing the product(s);
-
designing a sampling plan;
-
collecting the sample units;
-
analyzing the laboratory test samples; and
-
statistically analyzing the data and interpreting the results.
This chapter will address each of the five steps. Each of the steps can be performed in several different ways, and decisions made regarding the alternatives may directly impact the available resources, data quality (error in a data set), and the statistically defined risk of making a correct decision. Please note that this manual is not intended to be a statistics book or a comprehensive sampling text. Data base developers may need to consult the scientific literature, and in some cases, a statistician or research analyst to obtain additional detailed information that is relevant to the data base(s) of interest, but that is not contained in this manual.
This chapter, with the examples and definitions that are given, should serve as a general guide for individuals needing a basic reference concerning some of the administrative and statistical considerations that are associated with the development of a data base.
1. Characterizing the Product(s)
In characterizing the product, one should first determine the innate nutrient makeup of the product and obtain preliminary estimates of nutrient levels, nutrient variation, and the factors that could impact nutrient levels and variation. The first step in describing a product or products is to perform a literature search to determine if there are (1) existing nutrient data; (2) estimates that describe the market (production and sales); and, if appropriate, (3) information that describes the varieties (or species, if applicable); (4) the regions where the food is grown or raised; and (5) factors already studied and known to impact or not to impact nutrient levels. If the scientific literature and other sources reveal that a nutrient is known to be absent from the food or is present in negligible amounts (e.g., sugars and dietary fiber in seafood, cholesterol and saturated fat in produce), then the agency will not require testing for that nutrient, as long as the data base developer includes supporting documentation (58 FR 2079 at 2109, January 6, 1993).
If no information is available that adequately describes the food and its nutrients, the data base developer may choose to perform a pilot study to determine if certain factors do impact nutrient levels, to determine if there are regional differences in the nutrient levels, or to test for nutrient losses over time. In addition, the developer may choose to include other relevant factors of interest in a proposal to collect nutrient data for a data base study. For fruits and vegetables, variability may arise from seasonal and geographic influences associated with such factors as variety, location (e.g., soil type, climatic conditions); growing conditions (e.g., planting time, irrigation and fertilization practices, harvest maturity); product transport (e.g, packing, shipping, storage); and processing practices. For seafoods, the variability in nutrient levels may arise from such factors as species, dietary habits, processing practices, etc. For "mixed products", in addition to the factors that influence the variation in the nutrient levels in the product ingredients, processing factors associated with the formulation of the product ingredients into the "mixed product" may also influence the variation in the nutrient levels of the finished product. In some instances, if there is a great difference in nutrient values attributable to a particular factor (e.g., different nutrient values for different food types), a data base developer may determine that the foods are different and may even consider different nutrition labels for different food types.
When a data base developer submits a proposal to FDA, it is important to include the results of any pilot or experimental study that was completed. One data base developer, for example, completed a number of experimental studies that determined differences in nutrient levels between/among several independent variables (e.g., variety of food (2 levels), site of sampling (production vs. retail), packing medium (brine vs. water) , geographical region (5 levels), and age of product (5 levels)). FDA requests that the results of any experimental study that is submitted to the agency be included in statistical tables to better describe the type(s) of statistical test used, the sample size, and the exact probability levels that were used in drawing conclusions based on these results.
In determining the sampling plan (next section), existing nutrient data are extremely helpful in determining the number of samples to test.
2. Designing a Sampling Plan
Determining a Sample that is Representative of its Population
Once a manufacturer or other data base developer has a clear description of the product(s), the second step is to design a sampling plan. Attempting to collect and analyze all packages or units of a particular product is neither reasonable nor possible. Instead, the manufacturer or data base developer collects a sample, a subset of the population (i.e., the entire universe of all units of a product), using a sampling plan designed to provide a sample that is representative of the population. In turn, the conclusions that one draws from sample estimates should reflect the population in such a way that the sample isrepresentative of the population. In order for the sample to be representative of the population, the sampling plan must give consideration to the product descriptions, as specified earlier in this chapter. That is, the sampling plan should consider any factors that were determined to impact or that might possibly impact nutrient content of the product(s). In so doing, the data base may be designed to consider and select samples based on one or more factors that may impact on nutrient variability, or, preferably, on a combination of such factors. For example, if a data base concentrates on foods selected from one state, the sampling plan might include the collection of samples according to the regions within the state where the food is grown. In addition, because some foods are known to show seasonal variation in total fat content, a relevant data base would likely want to include samples harvested at selected seasons. Furthermore, in some instances, it may be appropriate to sample according to type of processing.
Determining the Point of Sampling
FDA determines compliance at the point of purchase. Because selected nutrients in some foods may undergo changes due to various factors (e.g., time after harvest or catch, processing, manufacture, conditions of transport), the agency recommends that food products be sampled at the point that is closest to the consumer. This point is typically defined at the retail or wholesale level. FDA acknowledges that, in certain circumstances, a data base developer may want to sample products at other positions along the production chain, such as the producer level. If the developer provides the agency with a sound justification for alternative sampling, in some instances, the agency may consider the alternative point of sampling as acceptable for the product(s) of interest.
Determining the Sampling Frame
The next step is to design a reasonable sampling frame. The sampling frame is a listing of the actual sampling units for a particular product population that provides a complete, accurate, and up-to-date coverage of the sampling units in the population. If a data base developer wishes to include several levels (stages) of sampling to take into account different factors, a separate sampling frame is necessary for each stage of sampling.
For example, if a data base developer wishes to provide a nationwide multi-stage survey of products selected at the retail level, the first stage sampling units (or primary sampling units (PSAs)) might be Metropolitan Statistical Areas (MSAs). MSAs delineate segments of the United States based on population size. MSAs were developed so that federal agencies would have standardized geographic definitions for reporting data for metropolitan areas. A detailed list of MSAs that defines the cities/counties that comprise each MSA can be found in the Federal Information Processing Standards Publication entitled "Metropolitan Statistical Areas (Including CSMAs, PMSAs, and NECMAs)," published by the National Institute of Standards and Technology. Because MSAs are divided into regions, one may say that the first stage is MSAs stratified by region. Stratification by region means that all regions will be included in the sampling process.
The second stage sampling units might then be at the retail level. Therefore, a listing of retail outlets within each of the selected MSAs might need to be developed or may be available from one of several private suppliers of business listings in the Unites States.
On the other hand, a data base developer may wish to divide the United States into states (first stage) stratified by region (all regions, the strata, will then be included), and then cities or towns within each state (second stage). Subsequently, the developer may wish to list retail outlets (third stage) and stratify by store type (chains vs independents) and store size (annual sales of at least $2 million vs. annual sales of less than $2 million). Sampling frame construction can be both time consuming and costly.
Determining the Sampling Methodology
FDA recommends that each data base developer use probability sampling methods, also referred to as random sampling. With random sampling, each element or subsample of the population has a known, nonzero, probability of being included in the sample, and the data base developer has a very good idea of the accuracy of estimates. To the extent that the sample is not a random sample, the estimates may be statistically meaningless, because statistical theory is based on random sampling. Several of the most commonly used probability sampling methods are simple random sampling; systematic sampling with a random start; stratified sampling; and cluster and multi-stage sampling. An overview of each method is beyond the scope of this manual but can be located as necessary in many textbooks describing research or survey methodology.
The data base developer should realize, however, that sampling is seldom simple. While simple random sampling will provide unbiased estimates of the mean and sampling errors, in developing a data base, this method will probably be used only in combination with other more complex sampling methods that take into account multi-stage sampling. When using multi-stage sampling, the data base developer should determine the stages and the number of sampling units to select within each stage. Example questions may include: How many regions within the U.S. will be sampled? How many MSAs or cities within each region will be sampled? How many warehouses, packers, shippers, and/or retail outlets will be sampled? How many lots will be sampled from each establishment? How many composite samples will be sampled from each lot? How many varieties or species should be sampled? When will the composite samples be selected? The questions continue . . .
How Many Composite Samples are Necessary?
At this point, the data base developer should begin to consider potential costs of laboratory analyses. A recent (1997) quote from a widely-recognized laboratory that analyzes food is $750 for the analysis of one composite sample for all required nutrients (see Nutrition Label on p. vi). Costs of specific analyses will likely vary and no doubt increase over time, but, for this edition of the nutrition labeling manual, the $750 per composite sample estimate will be used. Because of the significant costs associated with numerous analyses, the data base developer needs to be able to determine the minimum number of composite samples (with each composite composed of 12 retail units) needed to provide a valid data base and hence, valid nutrition labels.
There are a number of factors to consider in determining a sample size, that is, the minimum number of composites to analyze. As indicated in section 1 of this chapter, current or historical nutrient data that are available in the scientific literature or are collected through a pilot study may be used to estimate a sample size that fulfills predetermined criteria. Two formulas that may be used to estimate such sample sizes are described below.
Formula I: This formula infers that the true mean (nutrient value) of the population is within a given confidence interval of a specified width, for a simple random sample:
, where
n = the sample size you wish to calculate
z2 = the square of a value from a table of the normal distribution for a risk α
[For a 95% confidence level, use 1.96 and square it.]
σ2 = the square of the population standard deviation, which is the variance
ε2 = the square of the margin of error desired for the sample estimate
[ε = P μ; P is the relative error, e.g., 5% or 15%; μ is the mean]
The formula may be simplified to:
EXAMPLE: Nutrient data for sodium, potassium, and vitamin C were derived from a pilot study of 12 composites (12 samples of 12 units each) of a product. In order to derive the number of composites for a more comprehensive study to estimate the true mean of the nutrients within 5% [use P of .05], except for a 5% risk [use 1.96], consider the following calculations:
| Nutrient | Mean | Standard Deviation | CV = Standard Deviation / Mean | % CV |
|---|---|---|---|---|
| Sodium (mg) | 89.32 | 20.0 | 22.39 / 100 = .2239 | 22.39% |
| Potassium (mg) | 299.26 | 65.0 | 21.72 / 100 = .2172 | 21.72% |
| Vitamin C (mg) | 7.28 | 2.0 | 27.47 / 100 = .2747 | 27.47% |
Sodium:
= (1.96)2 (20)2 / (.05 x 89.32)2
= (3.8416) (400) / (4.466)2
= 1536.64 / 19.9452
= 77.0431 or 77
Potassium:
= (1.96)2 (65)2 / (.05 x 299.26)2
= (3.8416) (4225) / (14.963)2
= 16230.76 / 223.891
= 72.4940 or 72
Vitamin C:
= (1.96)2 (2)2 / (.05 x 7.28)2
= (3.8416) (4) / (.364 )2
= 15.3664 / .1325
= 115.9728 or 116
Formula II: This formula may be used when there is only an estimate of relative variation of the population (i.e., the population coefficient of variation, which is the population standard deviation divided by the population mean).
n = z2 (CV)2 / P2, where
n = the sample size you wish to calculate
z2 = the square of a value from a table of the normal distribution for a risk
[For a 95% confidence level, use 1.96 and square it.]
CV2 = the square of the coefficient of variation
P2 = the square of the relative error desired for the sample estimate, e.g., 5%
The formula may be simplified to: n = (1.96)2(CV)2 / P2
EXAMPLE: Estimates for the prior example are as follows:
Sodium:
= (1.96)2 (.2239)2 / (.05)2
= (3.8416) (501.3121) / (.0025)
= 1925.8406 / .0025
= 77.0336 or 77
Potassium:
= (1.96)2 (.2172)2 / (.05)2
= (3.8416) (.0471758) / .0025
= .1812 / .0025
= 72.48 or 72
Vitamin C:
= (1.96)2 (.2747)2 / (.05)2
= (3.8416) (.0754601) / .0025
= .2899 / .0025
= 115.96 or 116
Other Considerations
The sample sizes in the above examples were estimated under the assumption that a collective estimate (e.g., all apples), as opposed to subclass estimates (e.g., several varieties of apples), was needed. If subclass estimates are necessary, the sample sizes should be increased. For example, if there are 4 varieties (V = 4), and if nutrient estimates are desired for each variety at the same level of precision as for the overall sample, then the necessary sample size would be V times (4 times) as large as that if the varieties could be considered collectively. If the collective sample size is used, then the margin of error in the estimate for any one variety would equal the square root of V times the margin of error for the collective estimate, assuming equal sample sizes in the comparison. In the example above, the margin of error would be increased from .05 to .20.
Another consideration is the design effect, which is the ratio of the variance of an estimate (e.g., sample mean), based on a sampling method that is more complex (e.g., multi-stage sampling using stratification and/or clustering) than simple random sampling, to the variance of the estimate based on a simple random sample of the same size:
DE = s2 (complex random sampling) / s2 (simple random sampling)
The variance derived using the more complex sampling method is usually greater than the variance derived through simple random sampling; thus, the design effect would be greater than 1.
If an estimate of the design effect is available, it has utility in sample size estimation. For example, one may estimate the number of composites needed by assuming simple random sampling and then adjust this estimate by multiplying the design effect by the sample size. In the example above, if the design effect is 1.25, the number of composite samples would be n multiplied by 1.25, or 96, 90, and 144, respectively.
How Many Composite Samples Should You Analyze?
When the sample sizes for various nutrients vary, the data base developer may conduct the number of analyses corresponding to the number that were calculated for each individual nutrient. Another, but more costly, option would be to select the number of composites corresponding to the largest sample size estimate for the individual nutrients and analyze that number of samples for all nutrients.
Cost considerations are an important factor, particularly if data bases for several products are contemplated. For example, using the 1997 estimate of $750 (above), analysis of 144 samples could cost $108,000. There are several questions that should be asked at this point:
Are there any nutrients that are known to be absent from the product or that are present at insignificant levels? Awareness of such nutrients and supporting documentation regarding their levels may help reduce the number of analyses needed.
What is the time frame for the data base development? Total costs could be spread over several years if all analyses need not be conducted in one year.
How much risk of values being out of compliance is acceptable? Data collected from fewer composite samples can potentially provide estimates that are not as reliable as those obtained from a larger number of samples. Thus, there may be a greater risk of a label value being found out of compliance if only a small number of samples are analyzed.
Using the previous example, and considering a 90% confidence interval and a relative error of 15%, the estimates will change. Take the sodium data, for example:
Sodium:
= (1.645)2 (20)2 / (.15 x 89.32)2
= (2.706) (400) / (13.398)2
= 1082.4 / 179.5064
= 6.0299 or 6
Multiplying the 6 by a design effect of 1.25 gives you 7.5, which rounds to 8.
Assuming that the sample size estimates for the other nutrients were less than or equal to that for sodium, multiplying 8 by $750 gives a cost estimate of $6,000. The answer to the question of how much risk is acceptable must be provided by individual data base developers. FDA encourages each data base developer to provide the best data base(s) possible with available resources. If a data base developer considers that data from 144 composite samples, for example, approaches an unattainable gold standard, it is the developer's prerogative to choose to analyze the number of samples that he/she estimates is reasonable and to accept a greater risk of the product being out of compliance.
Putting it Together Thus Far: An Example
Let's say that you, as a data base developer, have decided to collect a national sample that will provide 144 composite samples of a food for analysis. You will use a multi-stage sampling plan that will ensure that all product samples are drawn from a representative cross section of the nation. In the first stage, for your primary sampling units, you might wish to consider all MSAs that are stratified by region. The second stage units might be stores that are stratified by store type (chain vs. independent). The third stage might be months, stratified by the four seasons.
In this example, you first (1) randomly select 18 of the 22 MSAs that USDA uses to collect data from wholesalers on raw fruit and vegetable arrivals, which you assume are sufficient to provide adequate geographic coverage. The 18 MSAs that you have selected are stratified over six regions.
| Region | MSA |
|---|---|
| Northeast | Boston, MA Buffalo, NY New York, NY |
| Mid-Atlantic | Baltimore, MD Cincinnati, OH Pittsburgh, PA Philadelphia, PA |
| Southeast | Atlanta, GA Columbia, SC Miami, FL New Orleans, LA |
| Midwest | Detroit, MI Chicago, IL |
| Southwest | Dallas, TX St. Louis, MO |
| Pacific | San Francisco, CA Seattle, WA Los Angeles, CA |
(2) For each of the MSAs that you have selected, you need to compile a sampling frame: a listing of stores that includes the name, address, and type of ownership (chain vs. independent). Because you will need to make two sample collections from each store (over seasons) and you need 144 composite samples, you now need to randomly select 72 stores (144 w 2 = 72). The 72 stores should be selected proportionally to the number of stores per strata (MSA x type of ownership). You will need to determine how many chains and how many independents are in each MSA and over all the MSAs and then compute the proportion of each store type.
(3) Once you have drawn a sample of 72 stores, you need to randomly select two lots from each store so that one month of each season will be included in the overall sample, stratified by and in proportion to the four seasons.
At this point, for each of the 144 composite samples, representing 144 lots, 12 consumer units are to be systematically selected (from each of the 72 stores during 2 months) with equal probability. Once all units are collected, you will have 1728 consumer units (144 composite samples of 12 units each). A summary of the example is delineated on the following table:
| Stage | Sampling Aspects | Definition of Aspects |
|---|---|---|
| First | Sampling Units Stratification Sample Allocation Sample Selection Number of MSAs |
MSAs Region Proportional to MSAs within Region Equal probability within strata 18 |
| Second | Sampling Units Stratification Sample Allocation Sample Selection Number of Stores |
Stores Type of Ownership (chain vs.independent) Proportional to stores within type of ownership Equal probability within strata 72 |
| Third | Sampling Units Stratification Sample Allocation Sample Selection Number of Month-Lots |
Month-lots (data collections) Seasons One month-lot per season (2 collections/store) Equal probability within strata 144 (1 month lots/year/store) (72 x 2) |
| Fourth | Sampling Units Clustering Sample Allocation Sample Selection Number of Units |
Consumer units Lots 12 units per lot Equal probability within lot 1728 (144 lots x 12 units) |
3. Collecting the Sample Units
The quality of the composite samples submitted for laboratory analysis can have a significant impact on the resultant data The best analytical capability available cannot restore the physical integrity (e.g., physical characteristics, nutrient content) of the laboratory sample if these or other qualities have been compromised during collection, handling, or shipping.
Sample Collection Procedure
Regardless of the sampling method chosen, the actual collection of the samples should be random. Random sampling is not haphazard sampling, during which the sampler arbitrarily selects the sample. Rather, random sampling is an objective process, which is used to select the units that are to be included in the sample. For example, if the units are in crates that are stacked in layers on pallets, obvious bias (error) would be introduced if the entire sample is drawn from only the top layer of crates on a single pallet or from only the top layer of crates on several pallets. It may be possible to eliminate or at least reduce bias by avoiding practices such as drawing units from the same position in crates, pallets, stacks, or piles.
Similarly, a sampler should not select units from one production line or sorting belt in lieu of others. If such sampling practices are avoided, the selected sample will, for practical purposes, approximate a random sample and will be more representative of the population than a sample collected in a non-random manner.
In bulk sampling situations in which the units have been thoroughly mixed, sorted, or arranged, a sample drawn anywhere from the bulk units may be considered random for practical purposes.
Logging the Laboratory Samples
whose responsible for collecting the samples should mark or tag them and maintain a log to record pertinent details about their history. This information should accompany the sample and the analytical results through the chain of custody. Details should include, as a minimum, and if appropriate for the product:
-
identification number (assigned by sampler)
-
name of the product
-
product variety
-
size or amount of product collected (referred to as the "increment")
-
place and date of collection
-
lot number or code
-
name and address of the grower, processor, distributor, shipper, supplier, retailer, etc.
-
description of the dispatch information (packing, shipping, and handling) sent to the analytical laboratory
-
any auxiliary information that will be needed in the statistical evaluation (e.g., stratum size, cluster size, etc.).
Shipping the Laboratory Samples
Packing, storage, and transportation are factors that may affect levels of specific nutrients in certain commodities. Deteriorative processes may affect the analytical estimates determined by the laboratory in such a way that the laboratory estimates may not adequately represent the nutrient levels in the population. In planning the sample collection activities, it is necessary to consider and incorporate suitable controls to reduce any adverse influence that these factors may have on data quality. Consideration should be given to the following:
-
nutrient stability and the storage life (perishability) of the product
-
adequacy of mode of transportation
-
type and size of shipping containers needed to properly store the product
-
type and amount of storage space needed
-
time needed to collect and prepare the laboratory samples for shipment
-
selection of the laboratory and knowledge of its priorities for analyzing the samples.
4. Analyzing the Laboratory Test Samples
Selecting an Analytical Laboratory
There are many laboratories in the United States that analyze food products for nutrition labeling purposes. It is beyond the scope of this manual to identify all such laboratories. The names and locations of appropriate laboratories can be found in publications of, for example, the Association of Official Analytical Chemists (AOAC), the American Association of Cereal Chemists (AACC), the American Oil Chemists Society (AOCS), and the Institute of Food Technologists (IFT), as well as in numerous trade journals and similar publications.
Laboratories performing nutrient analyses should be able to demonstrate that they operate under a documented Quality Assurance program that provides assurance that samples are adequately logged, stored, sampled, analyzed, and archived (if needed); that the integrity of the data collected is maintained; that analysts are appropriately trained; that equipment is calibrated; that analyses are conducted by appropriate calibrated methods and according to standard operating procedures; and that data are checked for errors and for reasonableness of results. Standard operating procedures for each method should include the use of Standard Reference Materials, spiked samples, or other validation materials (see below).
Composite Test Samples
An analytical laboratory generally performs single and replicate determinations on single composite and commingled composite test samples. A data base developer should be familiar with the purpose of making each type of measurement and should understand the effects of the sampling and analytical processes on the resultant data.
A single composite sample is a homogeneous mix of units of the same type (e.g., same variety, growing region, season, brand, lot). A commingled composite sample is a homogeneous mix of units of different types (e.g., different varieties, growing regions, seasons, brands, lots). Compositing, as it relates to nutrient analysis, is a process of physically averaging the concentrations of the nutrients in the units of the test sample.
As explained in Chapter I, for compliance purposes, FDA analyzes single composite samples based on 12 units each. Therefore, it is a good rule of thumb in developing a data base to include 12 units in each single composite sample that is tested. Regardless of the type of composite used, however, the laboratory should prepare the composite to contain the product in proportion to the sampled fraction for the product that is being composited.
Selecting the Analytical Methodology
For compliance purposes, FDA uses appropriate methods as given in the most recent edition of Official Methods of Analysis of AOAC International, or if no AOAC method is available or appropriate, by other reliable and appropriate analytical procedures (21 CFR 101.9 (g)(2)). AOAC International's current Official Methods volumes are updated annually with new or modified methods. In addition, results of successful collaborative studies appear in the J.Assoc.Offic.Anal.Chem. throughout the year.
Whenever possible, FDA uses AOAC Official Methods because such methods have undergone collaborative evaluations with respect to the following:
Accuracy: a measure of the closeness of agreement between the measured value and a value that is accepted as a "true" value or an accepted reference value;
Precision: a measure of the repeatability of the method under conditions of usual operation;
Specificity: the ability of the method to measure accurately and specifically the analyte of interest in the presence of other components that are expected to be present in the sample matrix;
Sensitivity: the limits of detection (LOD) and of quantification (LOQ);
Linearity (and range): the ability of the method to give results that are proportional to the analyte concentration within a specified range of concentrations.
The AOAC uses the terms repeatability and reproducibility to describe the variation in collaboratively studied methods under different circumstances of replication. Repeatability (i.e., precision) describes the agreement between successive results obtained by the same method on identical test samples under the same conditions (e.g., same analyst, apparatus, laboratory, reagents and time). Reproducibility (i.e., inter-laboratory precision) describes the agreement between individual results obtained with the same method on identical test material, but with different laboratories, instruments, analysts, reagents, and times. AOAC Official Methods also frequently identify the applicability of the method in terms of the matrices for which the method is suitable or those for which it is not.
For nutrition labeling, the limit of quantitation (LOQ) and not the limit of detection (LOD) is of primary interest. The LOD of a method is simply the lowest concentration of an analyte that can be detected, although not necessarily quantitated. The LOQ is the lowest level of analyte in the test sample that produces a signal sufficient to allow the determination of the analyte at least 95% of the time. Levels of nutrients above the LOQ will be measured with sufficient confidence to assign nutrition labeling values.
Alternative methodology is recommended only in the absence of AOAC Official Methods. If alternative methods are developed and/or used, they should be accompanied by documentation that describes in detail the analytical procedures and performance characteristics of the method.
Two references of particular usefulness in considering appropriate methods are Analyzing Food for Nutrition Labeling and Hazardous Contaminants by I.J. Jeon and W.G. Ikins (Marcel Dekker, Inc., New York, 1995, 496 pages) and Methods of Analysis for Nutrition Labeling, edited by D.M. Sullivan and D.E. Carpenter (AOAC International, Arlington, VA, 1993, 624 pages).
It is well recognized that modifications of AOAC Official Methods may be needed to comply with labeling requirements because Official Methods are not currently available for all nutrients of interest in all food matrices. Sullivan and Carpenter identify acceptable AOAC Official Methods for a wide range of nutrients, the matrices for which the methods are applicable, and current ideas on method adaptations. With appropriate modifications, some AOAC methods that appear to be of limited applicability can be modified for use with other food matrices. Jeon and Ikins' text is a valuable resource that describes the Official Methods available for the mandatory nutrients required on the new food labels and also describes analytical procedures for many nutrients that are considered optional for food labeling. The text also discusses the analysis of hazardous contaminants in foods. These two references provide valuable information for those interested in analytical methods for nutrients in foods.
When new methods are under development or when older methods are modified, the precision and accuracy of the new applications should be established. While precision can usually be demonstrated with replicate assays, determination of accuracy requires a material or a standard with a certified concentration of the analyte being measured. A chapter on use of Standard Reference Materials is included in the text by Sullivan and Carpenter (above).
A number of Standard Reference Materials available from the National Institute of Standards and Technology are certified for elemental composition and are representative of some foods (e.g., bovine liver, wheat flour, rice flour, tuna, spinach, etc.). Standard Reference Materials for some organic nutrients (e.g., oil and water-soluble vitamins in infant formula, cholesterol and vitamin A in coconut oil, cholesterol in whole egg, and fatty acids and cholesterol in a frozen diet composite) are also available.
Frequent use of Standard Reference Materials helps provide assurance of method performance, as does frequent use of in-house quality control materials. In-house quality control samples can be developed from large batches of well-characterized foods such as fortified cereals, specific oils, freeze-dried vegetables, chocolate chips, orange juice, or high-fiber cereals, to name several. Once the nutrient content of such materials has been established and the stability of the product ascertained, such materials can serve as excellent matrix- matched control materials.
Upon contacting an analytical laboratory for nutrient analysis for nutrition labeling purposes, the data base developer should ask the laboratory to provide a list of methods that the laboratory uses for analysis of each nutrient in the products to be submitted. The data base developer may wish to review the methods with FDA to determine if the proposed methods meet the standards for nutrition labeling.
5. Statistically Analyzing the Data and Interpreting the Results
Exploring the Data
The first step in working with any data set is to make sure that the data are clean, that is, virtually error free. In preparing the data for evaluation, quality control checks should be employed during the abstracting and coding of data to minimize the errors associated with these tasks. Possible errors may include inconsistencies and transcription errors, such as misreading data, decimal point errors, reversals of pairs of numbers, etc.
Once the data base developer determines that the data are error free, screening for outliers may be the next step. Outlier testing allows the identification of influential observations that may actually be transcription or analytical errors in the data. The agency is aware of the possible impact of outliers on analyses with other data points in a data set. Because it is critical that FDA understand the data that one may choose to delete from a data set, the agency requests documentation with accompanying rationale of all data that a data base developer wishes to delete. The agency also requests, however, a conservative approach to deletion of data. FDA does not currently have a policy on the preferred methodology for outlier detection, although there are various statistical and visual tests (e.g., box plots) for consideration. The agency hopes that as analytical methods improve over time and a data base developer collects more samples to update a data base, that estimates of nutrient levels will become more precise, and fewer observations will be out of line.
Calculating Label Values
FDA recommends that a data base developer consider the manner in which the data were collected and carry out the following steps in calculating a label value based on laboratory data: [Please note that the number of digits included for decimal places varies in the text. In order to minimize rounding error, it is better to keep as many decimal places as possible until a final value is calculated.]
-
Calculate the mean (average) nutrient content value from the analyzed nutrient values;
-
Calculate the standard deviation;
-
Convert the mean and standard deviation from a "per 100 g" basis to the label serving size that is required for the food;
-
Construct a one-sided 95% prediction interval;
-
Select the mean or predicted value for the nutrition label;
-
Calculate the percent daily value (DV) for appropriate nutrients; and
- Round the values according to FDA rounding rules.
1. Calculate the mean(average) nutrient content from the analyzed nutrient values
Calculate the mean nutrient content using procedures that are appropriate for the sampling procedure used to collect the samples. In the following example, the samples are assumed to be collected using a simple random sampling procedure. Assume that there are 12 laboratory values for protein from composites of raw broccoli, which were selected using this procedure from a production lot. The values per 100 grams (g) include: 2.8, 2. 5, 2.9, 3.5, 3.1, 4.1, 3.3, 3.1, 3.3, 2.8, 3.1, 2.8. To determine the mean, add the 12 values and divide by 12, or enter the data into computer software and allow the computer to do the calculation. An appropriate formula is:
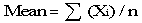
Σ (Xi) is the sum of the individual nutrient values in each laboratory analysis Xi and n is the number of analyses. For the broccoli example, the formula would be:
mean = (2.8 + 2.5 + 2.9 + 3.5 + 3.1 + 4.1 + 3.3 + 3.1 + 3.3 + 2.8 + 3.1 + 2.8) / 12 = 3.1083.
The mean protein content for broccoli would be 3.1083 g per 100 g. This value would be appropriate if the sample were drawn with equal probability of selection from the production lot.
2. Calculate the standard deviation
Calculate the standard deviation for nutrient content using procedures that are appropriate for the sampling procedure used to collect the samples. The standard deviation is a measure of the variability of the data. Data that are grouped close together will have a smaller standard deviation than would data that are spread out. Using a computer to calculate the standard deviation of a data set is by far the easiest method, but there are formulas to use if one chooses or if a computer is not available. One formula that may be used to estimate the standard deviation(s) for nutrient content is found in most basic statistics books and is:
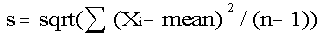
(number of) analyses
sqrt = the square root
This formula also assumes that the sample was collected as a simple random sample (i.e., equal probability of selection for each unit).
While the formula may look confusing, all that is necessary is to take each nutrient value and subtract the mean (3.1083) from it. Next square all the differences and add them. Then divide this quantity by the sample size minus 1 (11 in this example), and take the square root of the final number. The standard deviation of the protein values for broccoli in the current example is 0.4166061.
3. Convert the mean and standard deviation from a "per 100 g" basis to the label serving size that is required for the food
The Nutrition Labeling and Education Act of 1990 specified, in part, that the serving size used on product labels must be "an amount customarily consumed ... expressed in a common household measure that is appropriate to the food." Therefore, it is necessary to convert the data from a "per 100 g" basis to the appropriate serving size for the food. Serving sizes are determined using the procedures described in 21 CFR 101.9(b)(2) and are based on reference amounts customarily consumed per eating occasion (i.e., reference amounts) established in 21 CFR 101.12(b).
The serving size on the product label is expressed in a common household measure followed by the equivalent metric quantity (21 CFR 101.9(b)(7)). As stated in 21 CFR 101.9(b)(5), common household measures include cups, tablespoons, teaspoons, pieces, slices, fractions, ounces, fluid ounces, or other common household equipment used to package food products (e.g., jar, tray). When FDA performs nutrient analyses to determine the accuracy of nutrition labeling, assessment of compliance is based on the metric quantities that are part of the serving size declaration. Examples of serving sizes are provided below:
| Product | Reference Amount | Serving Size | |
|---|---|---|---|
| Soup | 145g | 1 cup (140) | |
| Cookies | 30g | 3 cookies (33g) | |
| Pizza | 140g | 1/4 pizza (150g) | |
| Bulk Cheese | 30g | 1 oz (28g / 1 inch cube) | |
For specific details of the final rules that apply to serving sizes, refer to the following sections of the Code of Federal Regulations:
| 21 CFR 101.9(b) | Nutrition labeling of food; definition of serving sizes |
|---|---|
| 21 CFR 101.9(b)(6) | Single- serving containers |
| 21 CFR 101.9(b)(8) | Number of servings per container |
| 21 CFR 101.12(b) | Reference amounts customarily consumed per eating occasion |
Other useful resources for determining serving sizes for product labels include: (1) A Food Labeling Guide; (2) Food Labeling - Questions and Answers; (3) List of products for each product category; and (4) Guidelines for determining metric equivalents of household measures. All four resources are found on FDA's web site at http://vm.cfsan.fda.gov.
Using the protein values included in the broccoli example above, you may convert each of the 12 nutrient values to a serving size basis (148 g for raw broccoli) and perform the calculations. It is far easier, however, to convert the mean and the standard deviation, which you have already calculated, from 100 g to 148 grams by using the following ratio:
To solve for Mean (148 g basis), the formula is:
Similarly, the standard deviation on a 100 g basis becomes s = 0.6165770 when it is expressed on the basis of 148 g.
4. Construct a one-sided 95% prediction interval
Prediction intervals aim at confidently bracketing the mean of any number (k) of future samples. From an FDA compliance perspective, the interval can contain the result of a single (k = 1) future retail unit or contain the mean of a number (k = 12) of future retail units. If a data base developer uses a 95% prediction interval to calculate label values, the food manufacturer is assured with 95% probability that if FDA tests the food for compliance purposes, the nutrients tested will meet compliance criteria. The one-sided aspect enters the equation because FDA wants the label to confidently state the minimum or maximum amount of a nutrient that may be expected in the product. To obtain this minimum or maximum label value, a component of the calculation is subtracted from the mean for class I and class II nutrients and added to the mean for nutrients in the third group.
Because of the potential variation in nutrient content of food products, food companies may choose to label the nutrient values on products conservatively, so that the products bearing these labels have a high probability of passing an FDA compliance evaluation. At the same time, consumers have the right to expect, with a reasonable probability, that label values will honestly and reasonably represent the nutrient content of the products that they purchase. In order to ensure that label values will have a high probability of being in compliance with nutrition labeling regulations and accurately represent the nutrient content of food products, FDA recommends the calculation of a one-sided 95% prediction interval as the most appropriate and the preferred method to use in computing label values, because products bearing mean values on their nutrition labels do not have a high probability of meeting FDA compliance requirements. Please note, however, that it is the manufacturer's choice whether to use a mean value or a predicted value on the nutrition label.
The following table outlines the equations used to compute predicted values for nutrients for the nutrient compliance classes:
| Nutrients | Equations |
|---|---|
| Class I (added) | predicted value = (mean - t (0.95;df) composite size/k + 1/n)1/2 (s)) |
| Class II (naturally occurring) | predicted value = (mean - t (0.95;df) (composite size/k + 1/n)1/2 (s))(5/4) |
| Third Group | predicted value = (mean + t (0.95;df) (composite size/k + 1/n)1/2 (s)) (5/6) |
where mean = the sample mean
t (0.95;df) = the one-tailed 95th percentile of the t-distribution with
df = the degrees of freedom, which is usually defined as n - 1
n = the number of samples analyzed
k = the number of future samples to be analyzed for the future mean (12 is recommended)
composite size = the number of units making up each composite in the data base used to compute the mean and s (12 is recommended)
The ratio of the composite size to k (composite size / k) reduces to 1 with 12 / 12
s = the standard deviation
The factors 5/4 or 5/6 represent, from the compliance viewpoint, the 20% margin of allowance in labeled values for class II nutrients or for the third group of nutrients, respectively.
The following t Table lists the t critical values at the one-tailed 95th percentile. Tables of the t-distribution may be found in any basic statistics book, although many only provide t values for samples sizes up to 31. The degrees of freedom (df) will vary depending on the number of samples (groups of data points) and the type of statistical analysis to be used.
| df | t | df | t | df | t | df | t |
|---|---|---|---|---|---|---|---|
| 1 | 6.314 | 11 | 1.796 | 21 | 1.721 | 35 | 1.691 |
| 2 | 2.920 | 12 | 1.782 | 22 | 1.717 | 40 | 1.684 |
| 3 | 2.353 | 13 | 1.771 | 23 | 1.714 | 45 | 1.679 |
| 4 | 2.132 | 14 | 1.761 | 24 | 1.711 | 50 | 1.676 |
| 5 | 2.015 | 15 | 1.753 | 25 | 1.708 | 60 | 1.671 |
| 6 | 1.943 | 16 | 1.746 | 26 | 1.706 | 70 | 1.667 |
| 7 | 1.895 | 17 | 1.740 | 27 | 1.703 | 80 | 1.664 |
| 8 | 1.860 | 18 | 1.734 | 28 | 1.701 | 90 | 1.662 |
| 9 | 1.833 | 19 | 1.729 | 29 | 1.699 | 100 | 1.660 |
| 10 | 1.812 | 20 | 1.725 | 30 | 1.697 | ∞ | 1.645 |
Predicted values will vary depending whether the data base developer has selected composite samples (e.g., 12 samples of 12) or individual samples (e.g., 12 individual samples). For analyses of composites: In the broccoli example, the following calculations apply for protein, a class II nutrient:
predicted value = (mean - t (0.95;df) (composite size/k + 1/n)1/2 (s)) (5/4)
= (4.6003 - 1.796 (12/12 + 1/12) 1/2(.6165770)) (5/4)
= (4.6003 - 1.796 (1.040833) (.6165770)) (5/4)
= (4.6003 - 1.1525896)(5/4)
= 3.4477104 (1.25)
= 4.309638
For analyses of individual units: Let's say that 12 individual units of broccoli were analyzed. The composite size would change in the formula from 12 to 1 because individual samples instead of composites are analyzed. Note the difference in the results.
predicted value = (mean - t (0.95;df) (composite size/k + 1/n)1/2 (12) 1/2 (s)) (5/4)
= (4.6003 - 1.796 (1/12 + 1/12)1/2 (.6165770)) (5/4)
= (4.6003 - 1.796 (.4082483) (.6165770)) (5/4)
= (4.6003 - 0.4520828)(5/4)
= 4.1482172 (1.25)
= 5.1852714
5. Select the mean or predicted value for the nutrition label
The agency recommends that the data base developer use one of two processes to determine whether to use the mean or the predicted value on the nutrition label. For some nutrients, depending on the nutrient class and the size of the mean relative to the predicted value, the mean might be chosen as the label value instead of the predicted value.
Process I: The first process is simple to use, as outlined on the following table:
| Nutrient | Selection Criteria |
|---|---|
| Class I and Class II | Select the lower of the mean or the predicted value |
| Third Group | Select the higher of the mean or the predicted value |
Protein is a class II nutrient. Because the mean (4.6003) is greater than the predicted value (4.309638), you would select the predicted value for the nutrition label for broccoli. [The rounded predicted value would be 4 g; a discussion of rounding will follow in section 7.] However, with analyzing individual units, the mean is smaller than the predicted value (5.1852714); in that case, you would select the mean for the nutrition label [actually, both would round to 5 g].
Process II: The second process that may be used to determine a nutrition label value considers the coefficient of variation (cv). The formula for the cv, expressed as a percent, is:
cv = 100 (s) / mean, where
s = the standard deviation
In the broccoli example above, the cv is (100 x .6165770) / 4.6003 =13.402974.
When the cv is small, the mean is more likely to be a candidate for selection as the label value. The upper limits of the cv have been calculated to show that, if the sample cv is smaller than the upper limit: 1) the predicted value for class II nutrients always exceeds the corresponding sample mean, and 2) the predicted value for the third group of nutrients is always less than the corresponding sample mean. The upper limits are related to the sample size and whether the nutrient analyses included individual units (12 individual units) or composite analyses (of 12 units each). The table below lists the upper limits of the cvs associated with use of the sample mean for label values. If the cv for your nutrient of choice is less than the upper limit on the table below, then the mean should be used on the label.
For the broccoli example, the cv rounds to 13. Because the data were analyzed as 12 composites of 12, the first step is to find 12, the sample size, under the first column of the table. Next you look at the third column (Upper Limit for 12-Unit Composites). If you follow the third column to the row indicating 12 samples, you find that the upper limit is 10.7. Because the cv (cv = 13) is greater than 10.7, you will select the predicted value for the nutrition label [4 g, as indicated above].
On the other hand, if the data were analyzed as 12 individual units, you follow the second column (Upper Limit for Individual Units) to the row indicating 12 samples, and find that the upper limit is 27.279. Because the cv (cv = 13) is less than 27.279, you will select the mean value for the nutrition label [5 g, as indicated above].
| Sample Size | Upper Limit for Individual Units |
Upper Limit for 12-Unit Composites |
Sample Size | Upper Limit for Individual Units |
Upper Limit for 12-Unit Composites |
|---|---|---|---|---|---|
| 5 | 17.625 | 8.564 | 33 | 35.026 | 11.632 |
| 6 | 19.851 | 9.189 | 34 | 35.196 | 11.648 |
| 7 | 21.641 | 9.628 | 35 | 35.358 | 11.662 |
| 8 | 23.128 | 9.958 | 36 | 35.512 | 11.676 |
| 9 | 24.391 | 10.203 | 37 | 35.659 | 11.689 |
| 10 | 25.481 | 10.403 | 38 | 35.800 | 11.702 |
| 11 | 26.435 | 10.565 | 39 | 35.935 | 11.713 |
| 12 | 27.279 | 10.700 | 40 | 36.065 | 11.725 |
| 13 | 28.031 | 10.813 | 41 | 36.189 | 11.735 |
| 14 | 28.708 | 10.911 | 42 | 36.307 | 11.745 |
| 15 | 29.319 | 10.995 | 43 | 36.422 | 11.755 |
| 16 | 29.875 | 11.068 | 44 | 36.531 | 11.764 |
| 17 | 30.383 | 11.133 | 45 | 36.637 | 11.773 |
| 18 | 30.849 | 11.190 | 46 | 36.739 | 11.781 |
| 19 | 31.279 | 11.242 | 47 | 36.837 | 11.790 |
| 20 | 31.676 | 11.288 | 48 | 36.931 | 11.797 |
| 21 | 32.045 | 11.329 | 49 | 37.022 | 11.805 |
| 22 | 32.387 | 11.367 | 50 | 37.110 | 11.812 |
| 23 | 32.707 | 11.402 | 51 | 37.195 | 11.819 |
| 24 | 33.006 | 11.434 | 52 | 37.277 | 11.825 |
| 25 | 33.287 | 11.463 | 53 | 37.357 | 11.831 |
| 26 | 33.550 | 11.490 | 54 | 37.433 | 11.837 |
| 27 | 33.798 | 11.515 | 55 | 37.508 | 11.843 |
| 28 | 34.032 | 11.538 | 56 | 37.580 | 11.849 |
| 29 | 34.252 | 11.559 | 57 | 37.650 | 11.854 |
| 30 | 34.461 | 11.579 | 58 | 37.717 | 11.860 |
| 31 | 34.659 | 11.598 | 59 | 37.783 | 11.865 |
| 32 | 34.847 | 11.616 | 60 | 37.847 | 11.870 |
6. Calculate the percent daily value (DV) for the appropriate nutrients
There are two sets of reference values for reporting nutrients in nutrition labeling: 1)Daily Reference Values (DRVs) and 2) Reference Daily Intakes (RDIs). These values assist customers in interpreting information about the amount of a nutrient that is present in a food and in comparing nutritional values of food products. DRVs are established for adults and children four or more years of age, as are RDIs, with the exception of protein. DRVs are provided for total fat, saturated fat, cholesterol, total carbohydrate, dietary fiber, sodium, potassium, and protein. RDIs are provided for vitamins and minerals and for protein for children less than four years of age and for pregnant and lactating women. In order to limit consumer confusion, however, the label includes a single term, i.e., Daily Value (DV), to designate both the DRVs and RDIs. Specifically, the label includes the % DV, except that the % DV for protein is not required unless a protein claim is made for the product or if the product is to be used by infants or children under four years of age. The following table lists the DVs based on a caloric intake of 2,000 calories, for adults and children four or more years of age.
| Food Component | DV |
|---|---|
| Total Fat | 65 grams (g) |
| Saturated Fat | 20 g |
| Cholesterol | 300 milligrams (mg) |
| Sodium | 2,400 mg |
| Potassium | 3,500 mg |
| Total Carbohydrate | 300 g |
| Dietary Fiber | 25 g |
| Protein | 50 g |
| Vitamin A | 5,000 International Units (IU) |
| Vitamin C | 60 mg |
| Calcium | 1,000 mg |
| Iron | 18 mg |
| Vitamin D | 400 IU |
| Vitamin E | 30 IU |
| Vitamin K | 80 micrograms µg |
| Thiamin | 1.5 mg |
| Riboflavin | 1.7 mg |
| Niacin | 20 mg |
| Vitamin B6 | 2 mg |
| Folate | 400 µg |
| Vitamin B12 | 6 µg |
| Biotin | 300 µg |
| Pantothenic acid | 10 mg |
| Phosphorus | 1,000 mg |
| Iodine | 150 µg |
| Magnesium | 400 mg |
| Zinc | 15 mg |
| Selenium | 70 µg |
| Copper | 2 mg |
| Manganese | 2 mg |
| Chromium | 120 µg |
| Molybdenum | 75 µg |
| Chloride | 3,400 mg |
In order to calculate the % DV, determine the ratio between the amount of the nutrient in a serving of food and the DV for the nutrient. That is, divide either the actual (unrounded) quantitative amount or the declared (rounded) amount (see next section) by the appropriate DV. When deciding whether to use the unrounded or rounded value, consider the amount that will provide the greatest consistency on the food label and prevent unnecessary consumer confusion. The nutrients in the table above are listed in the order in which they are required to appear on a label in accordance with 21 CFR 101.9(c). This list includes only those nutrients for which a DRV has been established in 21 CFR 101.9(c)(9) or a RDI in 21 CF 101.9(c)(8)(iv).
7. Round the values according to FDA rounding rules
The following table provides rounding rules for declaring nutrients on the nutrition label or in labeling:
| Nutrient | Increment Rounding | Insignificant Amount |
|---|---|---|
| Calories Calories from Fat Calories from Saturated Fat |
< 5="" cal="" -="" express="" as=""> ≤ 50 cal - express to nearest 5 cal increment > 50 cal - express to nearest 10 cal increment |
< 5=""> |
| Total Fat Saturated Fat Polyunsaturated Fat Monounsaturated Fat |
< .5="" g="" -="" express="" as=""> < 5="" g="" -="" express="" to="" nearest="" .5g=""> ≥ 5 g - express to nearest 1 g increment |
< .5=""> |
| Cholesterol | < 2="" mg="" -="" express="" as=""> 2 - 5 mg - express as "less than 5 mg" > 5 mg - express to nearest 5 mg increment |
< 2=""> |
| Sodium Potassium |
< 5="" mg="" -="" express="" as=""> 5 - 140 mg - express to nearest 5 mg increment > 140 mg - express to nearest 10 mg increment |
< 5=""> |
| Total Carbohydrate Dietary Fiber |
< .5="" g="" -="" express="" as=""> < 1="" g="" -="" express="" as="" "contains="" less="" than="" 1="" g"="" or="" "less="" than="" 1=""> ≥ 1 g - express to nearest 1 g increment |
< 1=""> |
| Soluble and Insoluble Fiber Sugars Sugar Alcohol Other Carbohydrate |
< .5="" g="" -="" express="" as=""> < 1="" g="" -="" express="" as="" "contains="" less="" than="" 1="" g"="" or="" "less="" than="" 1=""> ≥ 1 g - express to nearest 1 g increment |
< .5=""> |
| Protein | < .5="" g="" -="" express="" as=""> < 1="" g="" -="" express="" as="" "contains="" less="" than="" 1="" g"="" or="" "less="" than="" 1="" g"="" or="" to="" 1="" g="" if="" .5="" g="" to="">< 1=""> ≥ 1 g - express to nearest 1 g increment |
< 1=""> |
| When declaring nutrients other than vitamins and minerals that have RDIs as a % DV | express to nearest 1% DV increment | < 1%=""> |
| Vitamins & Minerals (express as % DV) |
< 2%="" of="" rdi="" may="" be="" expressed=""> ≤ 10% of RDI - express to nearest 2% DV increment |
< 2%=""> |
| Beta-Carotene (express as % DV) |
≤ 10% of RDI for vitamin A- express to nearest 2% DV increment > 10% - 50% of RDI for vitamin A- express to nearest 5% DV increment > 50% of RDI for vitamin A- express to nearest 10% DV increment |
To express nutrient values to the nearest 1 g increment, for amounts falling exactly halfway between two whole numbers or higher (e.g., 2.5 to 2.99 g), round up (e.g., 3 g). For amounts less than halfway between two whole numbers (e.g, 2.01 g to 2.49 g), round down (e.g., 2 g).
When rounding % DV for nutrients other than vitamins and minerals, when the % DV values fall exactly halfway between two whole numbers or higher (e.g., 2.5 to 2.99), the values round up (e.g., 3 %). For values less than halfway between two whole numbers (e.g., 2.01 to 2.49), the values round down (e.g., 2%).
When Data are Collected with Unequal Probability of Selection
The section of this chapter entitled Calculate the mean (average) nutrient content from the analyzed nutrient values explained how to calculate the mean when the sample was collected using a simple random sampling procedure, i.e., each sample had an equal probability of selection. In the following, we will expand this sampling procedure to provide an example of another sampling method: stratified sampling. Let's say, for simplicity's sake, that the samples for the previous example for broccoli were collected under the following scenario: a given producer is producing broccoli with two production lines that each account for 1/3 of the production, and that the remaining 1/3 of the production is accounted for by four other production lines that each account for 1/12 of the production. Further assume that a simple random sample of two composite samples of broccoli were collected from each production line. In this case, you will want to compute the weighted nutrient mean to account for the disproportionate sampling. The following is an example of the procedure needed to calculate the weighted mean and standard deviation for the amount of protein in the broccoli example cited under the current sampling scenario. The formula needed to calculate the weighted mean is as follows:
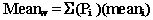
Pi = the proportion of the total production for line I
(i.e., given that N is the total production for all lines and Ni is the production for line I, then Pi = Ni / N)
The summation sign indicates that the results are summed over all production lines.
The formula needed to calculate the weighted standard deviation is as follows:
![s_w=sqrt{Sum[(P_i)^2(s_i)^2/n_i)(1-f_i)]}](https://public4.pagefreezer.com:443/content/FDA/16-06-2022T13:39/https://www.fda.gov/media/76775/download)
Pi2 = the square of the production proportion for line I
s2i = the variance of the ni protein values for the samples collected at line I
1- fi = the proportion of the samples at line i that were not included in the sample of size ni
Because each production line has associated with it a given number of degrees of freedom, it is necessary to compute the "effective degrees of freedom" (dfeff), ![df_eff=(s_w)^4/Sum[Z_i^2/(n_i - 1)]](https://public4.pagefreezer.com:443/content/FDA/16-06-2022T13:39/https://www.fda.gov/media/76778/download)
-
Compute for each production line the quantities Zi = (Pi2 ) (s2i /ni) (1-fi );
-
Obtain the sum of the Zi (Σ Zi) ;
-
Obtain the ratio
-
Square each Di and divide by the number of degrees of freedom (dfi = ni - 1) for production line I (Di2/dfi)
-
Obtain the sum of the Di2/dfi;
-
Take the recriprocal of this sum.
This result will be the "effective degrees of freedom" (dfeff) and should be used in determining the appropriate t-value for labeling calculations.
The following table lays out the calculations for the broccoli example, where the test samples were collected at the production lines with unequal probability of selection.
| (1) Prod. Line |
(2) Wgt. Pct. Total Vol. |
(3) Square Values in Col. (2) |
(4) Sample Size |
(5) Sample Fraction fi = ni w Line Volume |
(6) Nutrient Data Values |
(7) Nutrient Values Mean |
(8) Wgt. Times Mean |
(9) Var. of Sample Mean |
(10) Compute Zi |
|---|---|---|---|---|---|---|---|---|---|
| Pi | Pi 2 | ni | fi | yij | meani | (Pi) x (mean.i) |
s2i/ni | (Pi2 ) x (s2i /ni) x (1-fi ) |
|
| I | 1/3 | 1/9 | 2 | 0.01 | 2.8, 2.5 | 2.65 | 0.8833 | 0.0225 | 0.0025 |
| II | 1/3 | 1/9 | 2 | 0.01 | 2.9, 3.5 | 3.20 | 1.0667 | 0.0900 | 0.0099 |
| III | 1/12 | 1/144 | 2 | 0.04 | 3.1, 4.1 | 3.60 | 0.3000 | 0.2500 | 0.0017 |
| IV | 1/12 | 1/144 | 2 | 0.04 | 3.3, 3.1 | 3.20 | 0.2667 | 0.0100 | 0.0001 |
| V | 1/12 | 1/144 | 2 | 0.04 | 3.3, 2.8 | 3.05 | 0.2541 | 0.0625 | 0.0004 |
| VI | 1/12 | 1/144 | 2 | 0.04 | 3.1, 2.8 | 2.95 | 0.2458 | 0.0225 | 0.0002 |
| Total | 12 | 3.0166 | 0.0147 |
Having obtained the mean, standard deviation, and dfeff, one would use these results in computing the label values.
The previous example, although referring to production line sampling, reflects a stratified sampling procedure with production lines defining the strata. This procedure may be used when samples are either proportionally or disproportionally collected from strata that either naturally exist or can be meaningfully defined.
Chapter III: Ingredient Data Bases
As mentioned in Chapter I, an ingredient or "recipe" data base uses software to calculate label values derived from the ingredients that comprise a product's recipe, taking into account nutrient losses during processing.
Any association or manufacturer with an ingredient data base should also have a comprehensive quality management program which includes audits of ingredient nutrient data, product recipes, the software program, and final product analysis. Another crucial element is an ongoing program that compares nutrient data derived through laboratory analyses to ingredient data base calculations for finished products. Such comparisons are critical to cross validating the data that are used in a data base and to maintaining its integrity.
The agency does not currently have a policy on recommended procedures for comparing laboratory data to nutrient values calculated in an ingredient data base. One option would be to determine the percent of the nutrients where the laboratory and label values are equivalent when both are rounded. Another method would be based upon FDA compliance requirements, as specified in 21 CFR 101.9(g)(4). As indicated in Chapter I, in order to determine whether a nutrient value that is printed on a product package is in compliance, the agency completes laboratory analyses of the product and compares the nutrient values obtained through those analyses with the nutrient values provided on the package label. Specifically, that procedure, and one that a data base developer may wish to consider, is to examine the ratio between the laboratory value (unrounded) and the label value (rounded as included on the product package). Please note that error related to rounding is always a possibility.
FDA has adopted several principles relative to the development of ingredient composition data bases, which were recommended by companies and trade associations:
-
Confidence in the quality of data, supported by documentation of data sources.
Companies maintaining or using ingredient composition data bases should be able to demonstrate the data source used for each type of product and each nutrient for which ingredient composition data bases are utilized.
-
Proper maintenance of the data base.
Companies developing or using ingredient composition data bases should have procedures in place to ensure that the values in the ingredient composition data bases are reviewed and updated as needed and on a regular basis.
-
Specificity with respect to ingredients, product formulations and processes.
Companies using ingredient composition data bases should have procedures in place to ensure that the nutrient values are used only for specific applications. For example, a company should have a procedure to ensure that nutrient data specific for one product formulation or process are not used to prepare nutrient declarations for similar product formulations or processes, without assurance that the data are applicable to those products or processes.
-
Validation of the data base.
Companies developing or using ingredient composition data bases should have procedures in place to ensure that nutrient values receive reviews, audits, and confirmation through nutrient analyses as often as necessary.
Chapter IV: The FDA Data Base Review Process
In an effort to create a more efficient, flexible and responsive data base review system that would not overwhelm the resources that the agency has available, and yet provide industry with the assurance that it seeks through data base review and approval, FDA solicited comments regarding the agency's approach to data bases in a proposal on the voluntary nutrition labeling of raw produce and fish that it published in the Federal Register on July 18, 1994 (59 FR 36387). FDA carefully examined and fully considered the thoughtful comments submitted in response to the request and discussed those comments in the final rule on voluntary nutrition labeling of raw produce and fish that published on August 16, 1996 (61 FR 42742). Based on its review of the comments, FDA decided to modify its approach to data bases that are submitted to the agency for review. The new policy directly addresses concerns relevant to interim review and approval of data bases. At that time, the agency also implemented a new discretionary enforcement strategy for those manufacturers who submit interim data to the agency for approval.
Interim data in the form of nutrition label values that are submitted to the agency should be accompanied by raw data. If there are data that the manufacturer has determined as unsuitable, they should also be submitted with explanation. FDA will continue to evaluate interim data (i.e., historical or newly collected) submitted for review if those data are accompanied by a plan to collect additional data for the purpose of updating label values. However, in order to facilitate the use of the developing nutrient data base and to limit the uncertainty that could result from an unforeseen delay in agency review of the data base, firms will be free upon submission to begin use of the nutrient label values and to initiate the planned studies to collect and update nutrient values. Data submitted to FDA for the top 20 most frequently consumed raw fruits, vegetables and fish fall under the voluntary nutrition labeling program and will be reviewed and considered by the agency. However, only data published by FDA in appendices C and D to 21 CFR part 101 for those raw foods may be used for label and labeling purposes (21 CFR 101.45(b)). On the other hand, if a firm or association submits a data base for one of the top 20 raw fruits, vegetables, or fish that provides data to support optional nutrients (e.g., folic acid), the firm may use those data upon submission for label and labeling purposes. During this interim period, FDA does not anticipate that it will take action against a product bearing label values included in a data base submitted to the agency for review. If any product is identified through FDA compliance activities as including label values that are out of compliance, then, contingent on the company's willingness to come into compliance, the agency will work with both the manufacturer and the data base developer to understand and correct the problematic label values.
When FDA receives the interim data and planned studies referred to above, it will first evaluate the label values relative to the raw data. FDA will recalculate label values based solely on the raw data that have been submitted. The agency will derive label values using compliance calculations based upon 95 percent prediction intervals and, when appropriate, will use weighting procedures, as recommended in the nutrition labeling manual. FDA will evaluate the data for completeness and reasonableness (e.g., it will consider whether there are enough samples, and whether all nutrients are included). FDA requests that supporting documentation, such as analytical methodology and a sampling plan, accompany interim data. The agency acknowledges, however, that a large amount of the interim data available from manufacturers and trade associations are based upon historical data, for which the analytical methodology and sampling plan are not available. Hence, FDA will not refuse to accept data solely on the basis that it is not accompanied by comprehensive documentation, so long as the reason such documentation is not provided is fully explained and is acceptable to the agency.
FDA will review the accompanying planned studies to collect additional data, concentrating on analytical methodology and on the reasonableness of the factors that could account for nutrient variability (e.g., style, region), rather than on the rigor of sampling design or statistical treatment of the data. FDA suggests, however, that data base submitters should use as a guide the FDA recommendations regarding sampling strategies, weighting procedures, and statistical treatment of data that are described in the nutrition labeling manual.
FDA will respond in writing after review of the data and the planned studies. The agency will address the nutrient label values that were submitted and will notify the submitter whether it has any objection to continuing the planned studies or to continued use of the label values for two years from the date of the agency response. After those two years, manufacturers will be expected to provide the agency with a summary update that reassesses the interim label values based upon completion of the planned laboratory analyses. The agency will evaluate how the findings of the study relate to the interim label values and will consider whether it would have any objection to continued use of the updated interim values for up to an additional five years. At the same time, however, the agency may suggest modifications to the ongoing plan of study. If after review of data and planned studies, FDA determines that the label values or studies are not appropriate, as indicated above, the agency will notify the manufacturer of that decision. For the top 20 raw fruits, vegetables, and fish, FDA will consider all data that are submitted and may include those data in four-year updates to the list of foods and corresponding nutrient levels in Appendices C and D to 21 CFR part 101. For example, for the update to the regulation that is expected to publish in the year 2000, any data submissions should be provided to the agency by 1998 for inclusion in a proposed rule or afterward in a comment in response to that proposal.
Appendix: Numerical Examples
In Chapter II, section 2, there is an example that is included to show how to calculate the number of samples based on existing data. The following table provides a summary of hypothetical data derived from the calculated sample sizes. Assuming random sampling, the data may be used to calculate one-sided 95% prediction intervals and determine the appropriate label values. For the purposes of this example, also assume that the data are reported on a 100 g basis, the metric equivalent of the serving size is 110 g, and potassium and vitamin C are class II nutrients.
| Nutrient | Sample Size (n) | Mean | Standard Deviation (s) |
|---|---|---|---|
| Sodium | 96 | 87.1 mg | 25.25 |
| Potassium | 90 | 287.28 mg | 62.4 |
| Vitamin C | 144 | 6.95 mg | 1.87 |
Sodium
1) Convert the mean and standard deviation (s) to a serving size basis (110 g).
2) Calculate a one-sided 95% prediction interval.
predicted value = (mean + t (0.95;df) (composite size/k + 1/n)1/2 (s)) (5/6)
= (95.81 + 1.661 (12/12 + 1/96)1/2 27.775)) (.8333)
= (95.81 + 1.661 (1.0051948) (27.775)) (.8333)
= (95.81 + 46.373935) (.8333)
= (142.18394) (.8333)
= 118.48187, which rounds to 120 mg
The predicted value is larger than the mean; therefore, the label value for sodium should be the predicted value (120 mg). The % DV would be as follows: % DV = 120 / 2400 = .05 or 5% DV.
Potassium
1) Convert the mean and standard deviation (s) to a serving size basis (100 g).
2) Calculate a one-sided 95% prediction interval.
predicted value = (mean - t (0.95;df) (composite size/k + 1/n)1/2 (s)) (5/4)
= (316.008 - 1.662 (12/12 + 1/90)1/2 68.64) (1.25)
= (316.008 - 1.662 (1.0055402) (68.64)) (1.25)
= (316.008 - 114.71171) (1.25)
= (201.29629) (1.25)
= 251.62037, which rounds to 250 mg
The predicted value is smaller than the mean; therefore, the label value for potassium should be the predicted value (250 mg). The % DV would be as follows: % DV = 250 / 3500 = .0714286 or 7 % DV.
Vitamin C
1) Convert the mean and standard deviation (s) to a serving size basis (100 g).
2) Calculate a one-sided 95% prediction interval.
predicted value = (mean - t (0.95;df) (composite size/k + 1/n)1/2 (s)) (5/4)
= (7.645 - (1.656 (12/12 + 1/144)1/2 (2.057)) (1.25)
= (7.645 - (1.656 (1.0034662) (2.057)) (1.25)
= (7.645 - (3.4181993)) (1.25)
= (4.2268007) (1.25)
= 5.2835009, which rounds to 5 mg
The predicted value is smaller than the mean; therefore, the nutrient value for vitamin C should be the predicted value (5 mg). However, for vitamin C, only the % DV is reported on the nutrition label. The % DV would be as follows: % DV = 5 / 60 = . 0833 or 8 % DV.
1. This guidance has been prepared by the Office of Nutritional Products, Labeling, and Dietary Supplements (ONPLDS) and Office of Scientific Analysis and Support (OSAS) in the Center for Food Safety and Applied Nutrition (CFSAN) at the Food and Drug Administration (FDA). This guidance represents the Agency's current thinking on the development and use of nutrition labeling data bases. It does not create or confer any rights for or on any person and does not operate to bind FDA or the public. An alternative approach may be used if such approach satisfies the requirement of the applicable statute, regulations, or both.
We wish to acknowledge the assistance of Ellen Anderson, Ph.D., Carole Adler, M.A., R.D., and Virginia Wilkening, M.S., R.D., in the Office of Nutritional Products, Labeling, and Dietary Supplements, and Rene O'Neill and Jerome Schneidman, M.S., in the Office of Scientific Analysis and Support, in developing this manual. Users of this manual may submit comments to Office of Nutritional Products, Labeling, and Dietary Supplements, HFS-840, Center for Food Safety and Applied Nutrition, U.S. Food and Drug Administration, 200 C St., SW, Washington, DC 20204.
* Formulas may not show up correctly in text browsers. Please use a graphical browser or request a printed copy of this document from the following address:
Database Management and Evaluation Team (HFS-840)
Division of Research and Applied Technology
Office of Nutritional Products, Labeling, and Dietary Supplements
200 C Street, SW
Washington, DC 20204
(Tel) 202-205-5592
(Internet)http://www.cfsan.fda.gov/~dms/industry.html#lab
Final Rule: Change of Address; Technical Amendment, November 6, 2001
Effective December 14, 2001 the address for the Center for Food Safety and Applied Nutrition (CFSAN) is:
5001 Campus Drive
College Park, MD 20740-3835
Related Information
Submit Comments
You can submit online or written comments on any guidance at any time (see 21 CFR 10.115(g)(5))
If unable to submit comments online, please mail written comments to:
Dockets Management
Food and Drug Administration
5630 Fishers Lane, Rm 1061
Rockville, MD 20852
All written comments should be identified with this document's docket number: FDA-2020-D-1961.